1. נומער פון ציין Z די גאַנצע נומער פון ציין פון אַגאַנג.
2, מאָדולוס m דער פּראָדוקט פֿון דער צאָן־דיסטאַנץ און דער צאָל ציין איז גלייך צום אַרומנעם פֿון דעם טייל־קרייז, דאָס הייסט, pz= πd,

וואו z איז אַ נאַטירלעכע נומער און π איז אַן איראַציאָנעלע נומער. כּדי d זאָל זיין ראַציאָנעל, ווערט די באַדינגונג אַז p/π איז ראַציאָנעל גערופֿן דער מאָדולוס. דאָס הייסט: m=p/π
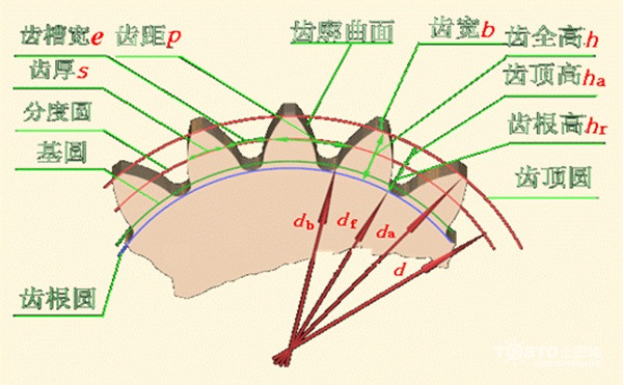
3, דער דיאַמעטער פון דעם אינדעקסירונג קרייז ד, די צאָן גרייס פון דעם גאַנג, ווערן באַשטימט באַזירט אויף דעם קרייז ד=mz קאָפּיע פול טעקסט 24, דער דיאַמעטער פון דעם אויבערשטן קרייז ד. און דער דיאַמעטער פון דעם וואָרצל קרייז דע פול פאַרשטעלן לייענונג פון די קאַלקולאַציע פאָרמולע פון ​​דער קאַם הייך און די וואָרצל הייך, די קאַלקולאַציע פאָרמולע פון ​​דעם קאַם קרייז דיאַמעטער און דעם וואָרצל קרייז דיאַמעטער קען זיין דערייווד:
ד.=ד+2ש.=מעז+2מ=מ(ז+2)

וואָס גרעסער דער מאָדולוס פֿון ראָד, אַלץ העכער און דיקער די ציין, אויב די צאָל ציין פֿון די

גאַנגאיז זיכער, די גרעסערע די ראַדיאַל גרייס פון די ראָד. מאָדולאַר סעריע סטאַנדאַרדס זענען פאָרמולירט לויט די באדערפענישן פון פּלאַן, מאַנופאַקטורינג און דורכקוק. פֿאַר גירז מיט נישט-גלייַך ציין, די מאָדולוס האט די חילוק צווישן די נאָרמאַל מאָדולוס mn, די ענד מאָדולוס ms און די אַקסיאַל מאָדולוס mx, וואָס זענען באזירט אויף די פאַרהעלטעניש פון זייער ריספּעקטיוו פּיטש (נאָרמאַל פּיטש, ענד פּיטש און אַקסיאַל פּיטש) צו PI, און זענען אויך אין מילימעטער. פֿאַר בעוועל גיר, די מאָדול די גרויס ענד מאָדול me, די דורכשניטלעך מאָדול mm און די קליין ענד מאָדול m1. פֿאַר די געצייַג, עס איז די קאָראַספּאַנדינג געצייַג מאָדולוס mo און אַזוי ווייטער. נאָרמאַל מאָדולס זענען וויידלי געניצט. אין די מעטריק גיר דרייוו, וואָרעם דרייוו, סינטשראָנאָוס גיר גאַרטל דרייוו און ראַטשעט, גיר קאַפּלינג, ספּליין און אנדערע טיילן, די נאָרמאַל מאָדולוס איז די מערסט גרונט פּאַראַמעטער. עס שפּילט אַ גרונט פּאַראַמעטער ראָלע אין די פּלאַן, מאַנופאַקטורינג און וישאַלט פון די אויבן טיילן.

1) דער מאָדולוס ווײַזט אָן די גרייס פֿון די ציין. דער R-מאָדול איז די פּראָפּאָרציע פֿון דער פּיטש פֿון דעם טייל־קרייז צום PI (π), אויסגעדריקט אין מילימעטער (מ״מ). אין דערצו צו מאָדולן, האָבן מיר דיאַמעטראַל פּיטש (CP) און DP (דיאַמעטראַל פּיטש) צו באַשרײַבן די גרייס פֿון די ציין. דער דיאַמעטראַל פּיטש איז די לענג פֿון דעם טייל־בויגן צווישן עקוויוואַלענטע פּונקטן אויף צוויי שכנותדיקע ציין.

2) וואָס איז "אינדעקס קרייז דיאַמעטער"? דער אינדעקס קרייז דיאַמעטער איז דער רעפערענץ דיאַמעטער פון דעםגאַנגדי צוויי הויפּט פאַקטאָרן וואָס באַשטימען די גרייס פון די גאַנג זענען די מאָדולוס און די נומער פון ציין, און דער דיאַמעטער פון די צעטיילונג קרייז איז גלייך צו די פּראָדוקט פון די נומער פון ציין און די מאָדולוס (ענד פּנים).
3) וואָס איז אַ "דרוק ווינקל"? דער שאַרפער ווינקל צווישן דער ראַדיאַלער ליניע ביים קנופּ פון דער צאָן פאָרעם און דעם צאָן פאָרעם טאַנגענט פון דעם פּונקט ווערט גערופן דער דרוק ווינקל פון דעם רעפערענץ קרייז. בכלל גערעדט, דער דרוק ווינקל באַציט זיך צום דרוק ווינקל פון דעם אינדעקסירונג קרייז. דער מערסט אָפט גענוצטער דרוק ווינקל איז 20°; אָבער, גירז מיט דרוק ווינקלען פון 14.5°, 15°, 17.5°, און 22.5° ווערן אויך גענוצט.

4) וואָס איז דער אונטערשייד צווישן איין-קאָפּ און צוויי-קאָפּ וואָרעם? די צאָל שפּיראַלישע ציין פון דעם וואָרעם ווערט גערופן די "צאָל קעפּ", וואָס איז גלייך צו דער צאָל ציין פון דעם גאַנג. וואָס מער קעפּ עס זענען, אַלץ גרעסער דער ווינקל פון דער פירערשאַפט.

5) ווי אזוי קען מען אונטערשיידן R (רעכט-האנטיג)? L (לינקס) גיר שטאנג ווערטיקאַל געשליפן פלאַך גיר צאָן נייגונג צו רעכטס איז דער רעכטער גיר, נייגונג צו לינקס איז דער לינקער גיר.

6) וואָס איז דער חילוק צווישן M (מאָדולוס) און CP (פּיטש)? CP (קייַלעכדיק פּיטש) איז די קייַלעכדיקע פּיטש פון די ציין אויף דעם אינדעקס קרייז. די איינהייט איז די זעלבע ווי דער מאָדולוס אין מילימעטער. CP צעטיילט דורך PI (π) גיט M (מאָדולוס). די באַציִונג צווישן M (מאָדולוס) און CP ווערט געוויזן ווי פאלגנד. M (מאָדולוס) =CP/π (PI) ביידע זענען איינהייטן פון צאָן גרייס. (דער צעטיילונגס אַרומקרייז = nd=zpd=zp/l/PI ווערט גערופן דער מאָדולוס

7) וואָס איז אַ "בעקלאַש"? די שפּאַלט צווישן די צאָן ייבערפלאַכן פון אַ פּאָר פון גירז ווען זיי זענען איינגעקנייטשט. בעקלאַש איז אַ נייטיק פּאַראַמעטער פֿאַר די גלאַט אָפּעראַציע פון ​​גיר מעשינג. 8) וואָס איז דער חילוק צווישן בייגן שטאַרקייט און צאָן ייבערפלאַך שטאַרקייט? בכלל, די שטאַרקייט פון גירז זאָל זיין באַטראַכט פון צוויי אַספּעקטן: בייגן און צאָן ייבערפלאַך שטאַרקייט. בייגן שטאַרקייט איז די שטאַרקייט פון די צאָן וואָס טראַנסמיטז מאַכט צו אַנטקעגנשטעלנ זיך די צאָן ברייקינג ביי די וואָרצל רעכט צו דער קאַמף פון בייגן קראַפט. די צאָן ייבערפלאַך שטאַרקייט איז די רייבשאַנאַל שטאַרקייט פון די צאָן ייבערפלאַך בעשאַס ריפּיטיד קאָנטאַקט פון די מעשעד צאָן. 9) אין די בייגן שטאַרקייט און צאָן ייבערפלאַך שטאַרקייט, וואָס שטאַרקייט איז געניצט ווי די באַזע פֿאַר סעלעקטינג די גיר? בכלל, ביידע בייגן און צאָן ייבערפלאַך שטאַרקייט דאַרפֿן צו זיין דיסקוטירט. אָבער, ווען סעלעקטינג גירז וואָס זענען געניצט ווייניקער אָפט, האַנט גירז, און נידעריק-גיכקייַט מעשינג גירז, עס זענען קאַסעס ווו בלויז בייגן שטאַרקייט איז אויסגעקליבן. לעסאָף, עס איז אַרויף צו די דיזיינער צו באַשליסן.